Mastering P Values: Your Ultimate Guide to Calculation and Interpretation

• Statistics
Quick Links:
• 1. Introduction to P Values
• 2. What is a P Value?
• 3. Importance of P Value in Statistics
• 4. How to Calculate P Value
• 5. Step-by-Step Guide to Calculating P Value
• 6. Case Studies: Understanding P Values
• 7. Common Misconceptions about P Values
• 8. Expert Insights on P Values
• 9. Conclusion
• 10. FAQs

1. Introduction to P Values

The P value is a vital concept in statistics, particularly in hypothesis testing. It serves as a measure of the strength of evidence against the null hypothesis. Understanding how to calculate and interpret P values is crucial for anyone involved in data analysis, research, or scientific inquiry. This article aims to provide a comprehensive understanding of P values, including their calculation, significance, and application in real-world scenarios.

2. What is a P Value?

The P value, or probability value, is the probability of observing results as extreme as those observed, under the assumption that the null hypothesis is true. A low P value indicates strong evidence against the null hypothesis, while a high P value suggests weak evidence. Typically, a threshold (alpha level) of 0.05 is used, but this can vary depending on the study.

Understanding the Null Hypothesis

The null hypothesis (H0) is a statement that there is no effect or no difference. It represents a default position that indicates no relationship between two measured phenomena. The P value helps researchers decide whether to reject this hypothesis.

3. Importance of P Value in Statistics

P values are crucial in various fields, including medicine, psychology, and social sciences. They help researchers determine statistical significance, guiding decisions based on data. However, relying solely on P values can be misleading; thus, they should be interpreted in context.

4. How to Calculate P Value

Calculating the P value can be approached through various methods depending on the type of data and hypothesis. Here are some common methods:

1. Using Statistical Software

Statistical software like R, SPSS, or Python can calculate P values easily. Here's a simple example using Python's SciPy library:

import scipy.stats as stats

# Sample data
data1 = [1, 2, 3, 4, 5]
data2 = [2, 3, 4, 5, 6]

# Perform t-test
t_stat, p_value = stats.ttest_ind(data1, data2)
print("P Value:", p_value)
    

2. Manual Calculation

For manual calculations, you can use the following formula depending on the test:

• For a one-sample t-test:
  P = 1 - t.cdf(T, df)
• For a two-sample t-test:
  P = 1 - t.cdf(T, df1 + df2 - 2)

3. Chi-Square Test

The chi-square test is another common method to calculate P values, especially in categorical data analysis. The formula is as follows:

# Chi-square test in Python
import scipy.stats as stats

# Observed values
observed = [10, 20, 30]
expected = [15, 15, 30]

# Calculate chi-square
chi2, p_value = stats.chisquare(observed, expected)
print("P Value:", p_value)
    

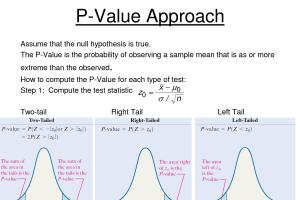
5. Step-by-Step Guide to Calculating P Value

Step 1: Formulate Hypotheses

Begin by defining your null and alternative hypotheses. For example:

• Null Hypothesis (H0): There is no difference between groups.
• Alternative Hypothesis (H1): There is a difference between groups.

Step 2: Choose the Right Statistical Test

Select the appropriate statistical test based on your data type:

• T-test for comparing means
• Chi-square test for categorical data
• ANOVA for comparing more than two groups

Step 3: Collect Data

Gather your data through experiments or observational studies. Ensure your sample size is adequate for reliable results.

Step 4: Calculate the Test Statistic

Use statistical software or manual calculations to compute the test statistic.

Step 5: Determine the P Value

Use the test statistic to find the P value using statistical tables or software.

Step 6: Interpret the Results

Compare the P value to your alpha level (commonly 0.05). If P < alpha, reject the null hypothesis.

6. Case Studies: Understanding P Values

Case Study 1: Medical Research

A recent study on a new drug showed a P value of 0.03, indicating significant efficacy compared to the placebo. This prompted further investigation into the drug's benefits.

Case Study 2: Educational Assessment

In a study comparing test scores between two teaching methods, a P value of 0.08 was found, suggesting no significant difference. Educators decided to explore other factors affecting performance.

7. Common Misconceptions about P Values

• P values do not measure the probability that the null hypothesis is true.
• A P value does not indicate the size or importance of an effect.
• Statistical significance does not imply practical significance.

8. Expert Insights on P Values

Experts emphasize the importance of context when interpreting P values. They advocate for complementing P values with confidence intervals and effect sizes for a comprehensive understanding of results.

9. Conclusion

Understanding how to calculate and interpret P values is essential for effective data analysis. This guide has provided a detailed overview of the concept, calculation methods, and practical applications. By mastering P values, researchers can make informed decisions based on statistical evidence.

10. FAQs

1. What does a P value of 0.05 mean?

A P value of 0.05 indicates that there is a 5% chance of observing the data if the null hypothesis is true. It is often used as a threshold for statistical significance.

2. Can P values be negative?

No, P values cannot be negative. They range from 0 to 1, representing probabilities.

3. What is a significant P value?

A P value less than the alpha level (commonly 0.05) is considered statistically significant, suggesting evidence against the null hypothesis.

4. Are P values the same as confidence intervals?

No, P values measure the evidence against a null hypothesis, while confidence intervals provide a range of values within which the true parameter likely falls.

5. How does sample size affect P values?

Larger sample sizes generally provide more reliable P values, as they reduce variability and increase the test's power.

6. When should I use a one-tailed vs. two-tailed test?

Use a one-tailed test when you have a specific direction of effect in mind. Use a two-tailed test if you are looking for any difference without a specific direction.

7. Can P values be misinterpreted?

Yes, P values can be misinterpreted. It's essential to understand that a low P value does not prove the alternative hypothesis; it only indicates evidence against the null hypothesis.

8. What is the relationship between P values and effect size?

While P values indicate statistical significance, effect size measures the magnitude of the difference. Both should be considered for comprehensive results interpretation.

9. How are P values used in clinical trials?

P values are used in clinical trials to determine the efficacy of treatments, comparing outcomes between control and treatment groups to assess significance.

10. What are some alternatives to P values?

Alternatives include Bayesian statistics, confidence intervals, and effect sizes, which provide a more nuanced understanding of data.

References

• P-Values: What They Are and How to Interpret Them
• Understanding P Values in Statistics
• Hypothesis Testing Explained
• Statistical Significance: Understanding P Values

Tags

• P value
• Calculate P value
• Statistical significance
• Hypothesis testing
• P value formula
• Statistics
• Data analysis
• Research methodology
• Significance level
• P-value calculator

You May Also Like