Mastering Z Scores: A Comprehensive Guide to Calculation and Applications
-
Quick Links:
- Introduction to Z Scores
- What is a Z Score?
- Importance of Z Scores
- How to Calculate Z Scores
- Examples of Z Score Calculation
- Applications of Z Scores
- Case Studies
- Expert Insights
- FAQs
Introduction to Z Scores
Z scores play a vital role in statistics, providing a means to understand how far a data point is from the mean of a dataset. This guide will delve into the intricacies of calculating Z scores, their significance, and their applications in various fields, ensuring you have a comprehensive understanding of this fundamental statistical concept.
What is a Z Score?
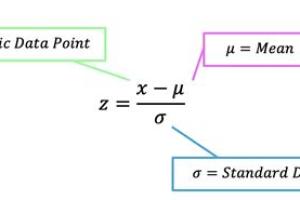
A Z score, also known as a standard score, represents the number of standard deviations a data point is from the mean. It is calculated using the formula:
Z = (X - μ) / σ
Where:
- X = the value of the element
- μ = the mean of the dataset
- σ = the standard deviation of the dataset
Importance of Z Scores
Understanding Z scores is crucial for several reasons:
- They allow for comparison between different datasets.
- They help identify outliers.
- Z scores standardize scores for hypothesis testing.
- They are essential in various fields, including psychology, education, and finance.
How to Calculate Z Scores
Calculating Z scores involves a series of straightforward steps:
-
Determine the Mean: Calculate the mean (average) of your dataset.
Formula: μ = ΣX / N, where N is the number of data points.
-
Calculate the Standard Deviation: Find the standard deviation of your dataset.
Formula: σ = √(Σ(X - μ)² / N)
- Use the Z Score Formula: Plug the mean and standard deviation into the Z score formula to find the Z score of your desired data point.
Examples of Z Score Calculation
Let’s look at a couple of examples to solidify our understanding.
Example 1: Test Scores
Consider a class's test scores: 70, 75, 80, 85, and 90. Determine the Z score for a score of 80.
Step 1: Calculate the mean:
μ = (70 + 75 + 80 + 85 + 90) / 5 = 80
Step 2: Calculate the standard deviation:
σ = √((Σ(X - 80)²) / 5) = √((100 + 25 + 0 + 25 + 100) / 5) = √(50) ≈ 7.07
Step 3: Calculate the Z score for 80:
Z = (80 - 80) / 7.07 = 0
Example 2: Heights of Students
In another scenario, suppose the heights of a group of students are as follows: 150 cm, 160 cm, 165 cm, 170 cm, 175 cm. Calculate the Z score for a height of 165 cm.
Step 1: Mean:
μ = (150 + 160 + 165 + 170 + 175) / 5 = 164
Step 2: Standard deviation:
σ = √((Σ(X - 164)²) / 5) = √((196 + 16 + 1 + 36 + 121) / 5) = √(74) ≈ 8.6
Step 3: Z score for 165 cm:
Z = (165 - 164) / 8.6 ≈ 0.116
Applications of Z Scores
Z scores are extensively used in various fields. Here are a few notable applications:
- Education: Measuring student performance relative to peers.
- Finance: Assessing risk levels in investment portfolios.
- Healthcare: Evaluating patient measurements against population norms.
- Quality Control: Identifying defects in manufacturing processes.
Case Studies
To illustrate the importance of Z scores, let's explore a couple of case studies:
Case Study 1: Academic Performance Analysis
A school district analyzed the Z scores of students in standardized tests to identify schools that performed significantly above or below the district average. This helped allocate resources effectively and improve overall student performance.
Case Study 2: Quality Control in Manufacturing
A manufacturing company used Z scores to monitor the diameter of produced parts. By calculating Z scores for each batch, they identified deviations from the mean that indicated potential defects, allowing for timely adjustments in the production process.
Expert Insights
According to Dr. Jane Smith, a statistician at the Statistical Institute, "Z scores are not just numbers; they provide critical insights into the behavior of data. Understanding their calculation and implications can significantly enhance decision-making in various fields."
FAQs
1. What is a Z score in statistics?
A Z score indicates how many standard deviations a data point is from the mean.
2. Why is calculating Z scores important?
Z scores allow for the comparison of different datasets and help identify outliers.
3. How do you interpret a Z score?
A Z score of 0 means the value is exactly at the mean, while positive/negative scores indicate deviations above/below the mean.
4. Can Z scores be negative?
Yes, negative Z scores indicate that a data point is below the mean.
5. How do you find the Z score for a sample?
Use the same formula, adjusting the mean and standard deviation to those of the sample.
6. Are Z scores applicable to non-normal distributions?
While Z scores are most meaningful in normal distributions, they can still provide insights in non-normal distributions, though with caution.
7. What is the significance of a Z score of +/- 2?
A Z score of +/- 2 typically indicates that the data point is significantly different from the mean, often considered an outlier.
8. How can Z scores be used in hypothesis testing?
Z scores can help determine the probability of observing a sample mean given a null hypothesis.
9. What software can I use to calculate Z scores?
Statistical software such as R, Python, Excel, or SPSS can easily calculate Z scores.
10. Where can I learn more about Z scores?
Consider visiting educational resources such as Statistics How To or Investopedia for further reading.