Mastering Statistics: A Comprehensive Guide to Mean, Standard Deviation, and Standard Error

• Statistics
Quick Links:
• Introduction
• What is Mean?
• How to Calculate Mean
• What is Standard Deviation?
• How to Calculate Standard Deviation
• What is Standard Error?
• How to Calculate Standard Error
• Case Studies and Examples
• Common Mistakes in Calculating Mean, Standard Deviation, and Standard Error
• Expert Insights
• Conclusion
• FAQs

Introduction

Statistics is a powerful tool that helps us understand and interpret data. Whether you are a student, researcher, or business professional, knowing how to calculate and interpret the mean, standard deviation, and standard error is essential. In this comprehensive guide, we will explore these statistical concepts in depth, providing you with step-by-step instructions, examples, and expert insights.

What is Mean?

The mean, often referred to as the average, is a measure of central tendency that summarizes a set of data points. It is calculated by adding all the values together and dividing by the number of values. The mean provides a quick snapshot of the data, helping to identify trends.

Key Characteristics of Mean

• It is sensitive to extreme values (outliers).
• It can be calculated for interval and ratio data.
• It may not represent the data well in skewed distributions.

How to Calculate Mean

Step-by-Step Guide

1. Collect your data set. For example, let’s consider the following data: 5, 10, 15, 20, 25.
2. Add all the numbers together: 5 + 10 + 15 + 20 + 25 = 75.
3. Count the number of values in the data set: 5.
4. Divide the total by the number of values: 75 / 5 = 15.
5. The mean of the data set is 15.

What is Standard Deviation?

Standard deviation is a measure of the amount of variation or dispersion in a set of values. It tells us how much individual data points deviate from the mean. A low standard deviation indicates that the data points tend to be close to the mean, while a high standard deviation indicates a wider spread of values.

Key Characteristics of Standard Deviation

• It is measured in the same units as the data.
• It is sensitive to outliers.
• It can be used to compare the spread of different data sets.

How to Calculate Standard Deviation

Step-by-Step Guide

1. Calculate the mean of your data set.
2. For each data point, subtract the mean and square the result.
3. Average the squared differences.
4. Take the square root of the average to find the standard deviation.

Example Calculation

Using the same data set: 5, 10, 15, 20, 25.

1. Mean = 15.
2. Squared differences: (5-15)² = 100, (10-15)² = 25, (15-15)² = 0, (20-15)² = 25, (25-15)² = 100.
3. Average of squared differences = (100 + 25 + 0 + 25 + 100) / 5 = 50.
4. Standard deviation = √50 ≈ 7.07.

What is Standard Error?

The standard error is a statistic that measures the accuracy with which a sample represents a population. It is the standard deviation of the sampling distribution of a statistic, most commonly the mean. A smaller standard error indicates a more precise estimate of the population mean.

Key Characteristics of Standard Error

• It decreases as the sample size increases.
• It provides insight into the reliability of the sample mean.
• It can be used to construct confidence intervals.

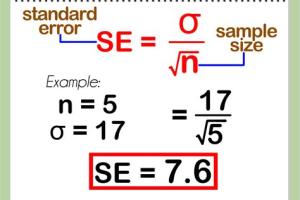
How to Calculate Standard Error

Step-by-Step Guide

1. Calculate the standard deviation of your sample.
2. Divide the standard deviation by the square root of the sample size.

Example Calculation

Using our previous example with a standard deviation of 7.07 and a sample size of 5.

1. Standard error = 7.07 / √5 ≈ 3.16.

Case Studies and Examples

Understanding how to calculate mean, standard deviation, and standard error is crucial in various fields such as education, psychology, and business. Let’s explore some real-world applications.

Case Study 1: Educational Testing

A school district wants to analyze test scores from its students. By calculating the mean score, they can identify the average performance. The standard deviation will reveal how much the scores vary, and the standard error will help understand the reliability of the mean score.

Case Study 2: Market Research

A company surveys consumer preferences for a new product. They calculate the mean rating of the product and the standard deviation to understand variability in responses. The standard error will help the company know how accurately their sample represents consumer sentiment.

Common Mistakes in Calculating Mean, Standard Deviation, and Standard Error

• Forgetting to account for outliers when calculating the mean.
• Using the wrong formula for standard deviation.
• Confusing standard deviation with standard error.

Expert Insights

Experts emphasize the importance of understanding the context of your data when interpreting these statistics. A statistician might recommend visualizing the data through graphs to enhance understanding before diving into calculations.

Conclusion

Calculating mean, standard deviation, and standard error are foundational skills in statistics that enable researchers and analysts to make informed decisions based on data. By mastering these calculations, you can improve your data analysis skills and contribute valuable insights in your field.

FAQs

1. What is the difference between mean and median?

The mean is the average of a data set, while the median is the middle value when the data is sorted. The median is less affected by outliers.

2. How does sample size affect standard error?

A larger sample size decreases the standard error, leading to a more accurate estimate of the population mean.

3. Can standard deviation be negative?

No, standard deviation cannot be negative as it is a measure of dispersion based on squared differences.

4. What is a good standard deviation?

A "good" standard deviation depends on the context and nature of the data. It should be interpreted relative to the mean and the data set.

5. How is standard error used in hypothesis testing?

Standard error is crucial in hypothesis testing as it helps determine the variability of sample means, facilitating the calculation of confidence intervals and significance tests.

6. What are the limitations of using mean as a measure of central tendency?

The mean can be skewed by extreme values (outliers), making it less representative of a data set with such values.

7. How can I visualize the standard deviation?

Standard deviation can be visualized using a bell curve (normal distribution) or by creating box plots that show the spread of data.

8. Why is it important to calculate standard error?

Calculating standard error is important as it provides insight into the precision of the sample mean as an estimate of the population mean.

9. Are there different types of standard deviation?

Yes, there are different types, including population standard deviation and sample standard deviation, which use different formulas based on the data set.

10. How can I calculate these statistics using software?

Many statistical software packages, such as SPSS, R, and Python (using libraries like NumPy and pandas), can calculate mean, standard deviation, and standard error easily.

For more information, check out resources from reputable sources:

• Mean - Statistics How To
• Standard Deviation - Statistics How To
• Standard Error - Investopedia

Tags

• Mean
• Standard Deviation
• Standard Error
• Statistics
• Data Analysis
• Math
• Education
• Calculation
• Research
• Data Science

You May Also Like