Mastering the Standard Error of Estimate (SEE): A Comprehensive Guide
-
Quick Links:
- Introduction
- Understanding the Standard Error of Estimate (SEE)
- Importance of SEE in Statistical Analysis
- Calculating the Standard Error of Estimate
- Step-by-Step Guide to Calculate SEE
- Examples of SEE Calculation
- Real-World Case Studies
- Common Misconceptions about SEE
- Expert Insights on SEE
- Conclusion
- FAQs
Introduction
The Standard Error of Estimate (SEE) is a pivotal concept in statistics, particularly within the realms of regression analysis and predictive modeling. It provides insight into the precision of a regression model by measuring the extent of error between observed values and predicted values. As we delve deeper into this guide, we will explore how to calculate SEE, its applications, and much more.
Understanding the Standard Error of Estimate (SEE)
The Standard Error of Estimate quantifies the accuracy of predictions made by a regression model. It is defined as the standard deviation of the residuals (the differences between observed and predicted values). In simpler terms, a lower SEE indicates that the regression model is a better fit for the data.
Key Terms Related to SEE
- Residuals: The differences between observed and predicted values.
- Regression Analysis: A statistical method for modeling the relationship between a dependent variable and one or more independent variables.
- Standard Deviation: A measure of the amount of variation or dispersion of a set of values.
Importance of SEE in Statistical Analysis
The SEE is crucial in assessing the reliability of a regression model. It helps researchers and analysts determine how well the model predicts outcomes. A smaller SEE indicates greater predictive accuracy, making it a vital metric in fields such as economics, healthcare, and social sciences.
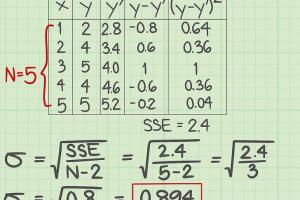
Calculating the Standard Error of Estimate
To calculate the SEE, follow these steps:
- Collect your data points for both independent and dependent variables.
- Perform a regression analysis to obtain the predicted values.
- Calculate the residuals (observed - predicted values).
- Square each residual and sum these squared values.
- Divide this sum by the degrees of freedom (n - k - 1, where n is the number of observations, and k is the number of predictors).
- Take the square root of the result to obtain the SEE.
Step-by-Step Guide to Calculate SEE
Step 1: Data Collection
Gather your data, ensuring it is clean and structured. For example, if you are predicting sales based on advertising spend, collect both datasets accurately.
Step 2: Perform Regression Analysis
Use statistical software (like R, Python, or Excel) to conduct regression analysis. This will give you the predicted values based on your independent variables.
Step 3: Calculate Residuals
For each data point, subtract the predicted value from the observed value. This will give you the residuals.
Step 4: Sum of Squared Residuals
Square each residual and sum them up. This gives you an indication of the overall error in your predictions.
Step 5: Calculate Degrees of Freedom
Use the formula n - k - 1 to calculate the degrees of freedom, essential for the next step.
Step 6: Calculate SEE
Divide the sum of squared residuals by the degrees of freedom and take the square root. This final value is your Standard Error of Estimate.
Examples of SEE Calculation
Example 1: Simple Linear Regression
Imagine you have a dataset where you want to predict sales based on advertising spend. After conducting regression analysis, you find the following:
- Observed Sales: [200, 250, 300, 400]
- Predicted Sales: [220, 260, 290, 390]
Calculating residuals gives you: [-20, -10, 10, 10]. Squaring these gives [400, 100, 100, 100]. The sum is 700. If you have 4 data points and 1 predictor, degrees of freedom = 4 - 1 - 1 = 2, leading to:
SEE = √(700 / 2) = 18.71
Real-World Case Studies
Here, we will explore some real-world applications of SEE to understand its impact.
Case Study 1: Healthcare Predictive Analytics
In a recent study, researchers used SEE to evaluate the accuracy of models predicting patient outcomes based on treatment methods. Their findings highlighted how an accurate SEE can assist in making informed decisions about patient care.
Case Study 2: Economic Forecasting
Economists rely heavily on regression models to predict market trends. A thorough understanding of SEE allowed them to refine their models, resulting in more accurate economic forecasts.
Common Misconceptions about SEE
Despite its importance, several misconceptions surround the Standard Error of Estimate:
- Misconception 1: SEE is the same as standard deviation.
- Misconception 2: A lower SEE always means a better model.
- Misconception 3: SEE can be used alone to validate a regression model.
Expert Insights on SEE
Experts in statistics emphasize the importance of SEE in validating predictive models. They suggest complementing SEE with other metrics, such as R-squared, to ensure a holistic view of model performance.
Conclusion
The Standard Error of Estimate is a crucial metric in the realm of statistics and analytics. Understanding how to calculate and interpret SEE can significantly enhance the reliability of your predictive models, enabling better decision-making across various fields.
FAQs
1. What is the Standard Error of Estimate (SEE)?
SEE measures the accuracy of predictions made by a regression model, indicating how much observed values deviate from predicted values.
2. How is SEE calculated?
SEE is calculated by taking the square root of the sum of squared residuals divided by the degrees of freedom.
3. Why is SEE important?
SEE helps assess the reliability of a regression model and its predictive accuracy, which is vital in data-driven decision-making.
4. Can SEE be used alone to evaluate a model?
No, SEE should be used alongside other metrics, such as R-squared, to validate the model comprehensively.
5. What is a good SEE value?
A lower SEE value indicates better model accuracy, but the acceptable level can vary depending on the context and data.
6. How does SEE differ from standard deviation?
SEE specifically measures prediction accuracy in regression models, while standard deviation measures the variability of a dataset.
7. Can SEE be negative?
No, SEE cannot be negative as it is derived from squared values, which are always non-negative.
8. What are residuals in relation to SEE?
Residuals are the differences between observed and predicted values, which are essential for calculating SEE.
9. How does sample size affect SEE?
A larger sample size can lead to a more accurate estimate of SEE, as it provides a better representation of the underlying population.
10. What software can be used to calculate SEE?
Software like R, Python, and Excel can be used for regression analysis and SEE calculation.