Mastering Statistical Significance: A Comprehensive Guide to Assessment

• Statistics
Quick Links:
• Introduction
• Understanding Statistical Significance
• Hypothesis Testing Explained
• What is a P-Value?
• Confidence Intervals and Their Importance
• Understanding Effect Size
• Common Mistakes in Assessing Significance
• Case Studies
• Step-by-Step Guide to Assessing Statistical Significance
• Conclusion
• FAQs

Introduction

Statistical significance is a crucial concept in research, helping determine whether the results of a study are likely due to chance or reflect genuine effects. This comprehensive guide aims to clarify how to assess statistical significance effectively, exploring various methods, common pitfalls, and practical examples.

Understanding Statistical Significance

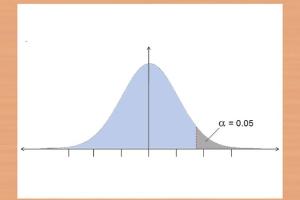
Statistical significance helps researchers determine if the results of their experiments or studies are meaningful. A result is typically considered statistically significant if the probability of it occurring by chance is less than a predetermined threshold, often set at 0.05 or 0.01.

Key Concepts

• Null Hypothesis (H0): The assumption that there is no effect or difference.
• Alternative Hypothesis (H1): The hypothesis that there is an effect or difference.
• Significance Level (α): The threshold for deciding whether to reject the null hypothesis.

Hypothesis Testing Explained

Hypothesis testing is a statistical method that uses sample data to evaluate a hypothesis about a population parameter. The process involves several steps:

1. Formulate the null and alternative hypotheses.
2. Select a significance level (α).
3. Collect data and compute the test statistic.
4. Determine the p-value.
5. Make a decision based on the p-value and significance level.

What is a P-Value?

The p-value measures the strength of the evidence against the null hypothesis. A smaller p-value indicates stronger evidence, typically leading researchers to reject the null hypothesis.

Interpreting P-Values

Here’s how to interpret p-values:

• P ≤ α: Reject the null hypothesis; results are statistically significant.
• P > α: Do not reject the null hypothesis; results are not statistically significant.

Confidence Intervals and Their Importance

Confidence intervals provide a range of values that likely contain the population parameter. They complement p-values by offering additional information about the precision and reliability of the estimate.

Constructing Confidence Intervals

To construct a confidence interval, you need:

• The sample mean (or another estimate).
• The standard error of the mean.
• The critical value from the Z or t distribution.

The general formula for a confidence interval is:

CI = Sample Mean ± (Critical Value * Standard Error)

Understanding Effect Size

Effect size measures the strength of a relationship or the magnitude of an effect. Unlike p-values, effect sizes provide context about the practical significance of results.

Types of Effect Size

• Cohen's d: Measures the difference between two means in terms of standard deviation.
• Pearson's r: Measures the strength and direction of a linear relationship between two variables.

Common Mistakes in Assessing Significance

Researchers often make several mistakes when assessing statistical significance, including:

• Misinterpreting p-values.
• Neglecting the power of a test.
• Overemphasizing statistical significance without considering practical significance.

Case Studies

Examining real-world cases can enhance understanding of statistical significance. Here are two examples:

Case Study 1: Medical Trials

In a clinical trial testing a new drug, researchers found a p-value of 0.03, indicating strong evidence against the null hypothesis. However, the effect size was small, suggesting that while the results were statistically significant, they may not have practical implications for patient care.

Case Study 2: Marketing Research

A marketing team conducted an A/B test on two different email campaigns. They found a p-value of 0.04 when comparing open rates. The confidence interval suggested a meaningful increase in engagement, leading to a decision to adopt the new email strategy based on both statistical significance and effect size.

Step-by-Step Guide to Assessing Statistical Significance

Here’s a detailed, step-by-step approach to assess statistical significance:

Step 1: Define Your Hypotheses

Clearly outline your null and alternative hypotheses.

Step 2: Choose a Significance Level

Decide on a significance level (α), commonly set at 0.05.

Step 3: Collect and Analyze Data

Gather your data, ensuring it is appropriate for the statistical tests you plan to use.

Step 4: Calculate the Test Statistic

Depending on the test (e.g., t-test, chi-squared test), calculate the relevant test statistic.

Step 5: Determine the P-Value

Use statistical software or tables to find your p-value.

Step 6: Interpret the Results

Compare the p-value to your significance level and draw conclusions.

Step 7: Report Your Findings

Present your results, including p-values, confidence intervals, and effect sizes, to provide a comprehensive view of your findings.

Conclusion

Assessing statistical significance is vital for making informed decisions based on data. By understanding the concepts of hypothesis testing, p-values, confidence intervals, and effect sizes, researchers can draw meaningful conclusions from their studies. Avoiding common pitfalls and applying a systematic approach will enhance the reliability of your results.

FAQs

1. What is the significance level?

The significance level (α) is the threshold for rejecting the null hypothesis, commonly set to 0.05.

2. How do I interpret a p-value?

A p-value indicates the probability of observing your data if the null hypothesis is true; lower values suggest stronger evidence against the null hypothesis.

3. What is the difference between statistical and practical significance?

Statistical significance indicates that results are unlikely due to chance, while practical significance assesses the real-world relevance of the findings.

4. Can I have statistical significance without practical significance?

Yes, results can be statistically significant but may not have meaningful implications in practice, especially with small effect sizes.

5. What is a confidence interval?

A confidence interval is a range of values that likely contains the population parameter, providing insight into the precision of your estimate.

6. How do I calculate effect size?

Effect size can be calculated using formulas specific to the type of data and analysis, such as Cohen's d for comparing means.

7. What are common mistakes in hypothesis testing?

Common mistakes include misinterpreting p-values, neglecting the power of a test, and overemphasizing statistical significance without considering effect size.

8. How do sample size and power relate to statistical significance?

A larger sample size increases the power of a test, making it easier to detect a true effect, and thus, more likely to achieve statistical significance.

9. What software can I use for statistical analysis?

Popular software options include R, Python, SPSS, and SAS, all of which have functions for conducting various statistical tests.

10. Why is it important to report effect sizes?

Reporting effect sizes helps convey the practical significance of findings, providing context beyond mere statistical significance.

Tags

• Statistical significance
• Assessing significance
• Hypothesis testing
• P-value
• Confidence intervals
• Data analysis
• Statistics guide
• Research methods
• Statistical testing
• Data interpretation

You May Also Like